第五章 神经网络

作者：韩歆哲

什么是前馈神经网络

对于模式识别主要有两类问题

• 分类: 找到一个分类方程；
• 回归：找到一个回归方程。
  他们的本质都是学习得到一个能够解决问题的方程表达式。

  神经网络的基本结构与传统统计机器学习方法的关系

  前面讨论过的传统统计学习方法，包括LR，感知机等模型，本质上是将变量本身，或者通过变量组合得到的特征（基函数）进行线性组合得到线性或者非线性的分类界面：

$$y(\mathrm{x}, \mathrm{w}) = f\left( \sum_{j=1}^M \omega_j\phi_j( \mathrm{x} ) \right)$$

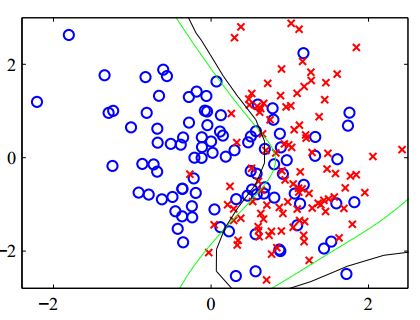
前馈神经网络的典型模型如下图

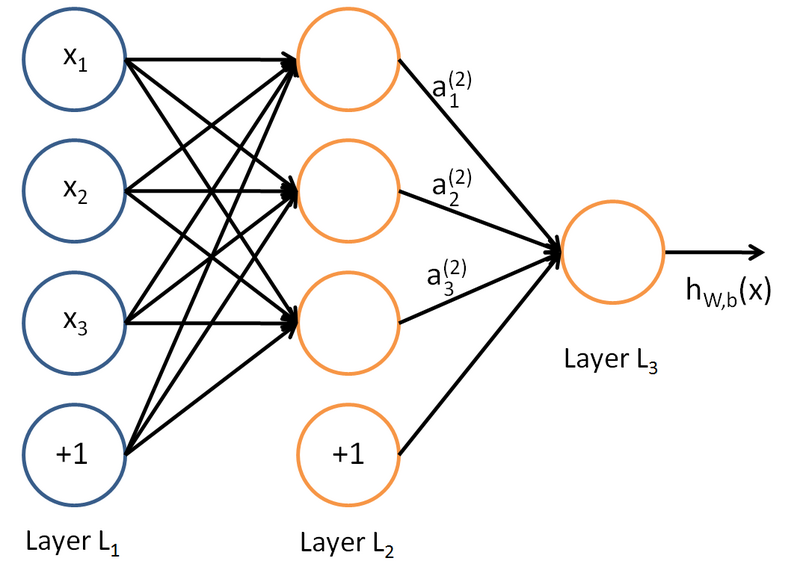
每个神经元的值是前一个神经元值的加权组合，写出多层神经网络的输出的表达式可以得到：

$$y_k = h_l\left(\sum_{j=0}^M \omega_{kj}^l h_{l-1}\left( \sum_{i=0}^D \omega_{ji}^{l-1}\cdots\right)\right)$$

将表达式与前面学习的方法进行对比，可以发现神经网络实际上就是将传统方法模型级联，得到了表达能力更强的方程表达。用三层神经网络拟合一个正弦曲线的示意图如下：

上图中的虚线表示隐藏层神经元的值，从数学表达上看，三条线可以作为正弦函数的基函数，从物理意义上看可以作为正弦曲线的“特征”。神经网络拥有远超传统方法表达能力的原因就是传统方法需要自己设计基函数或者说是特征，而神经网络通过增加的隐藏层可以根据数据学习得到使得误差最小的特征，因此在相同参数数量条件下函数的表达能力更强。

网络的前馈方程

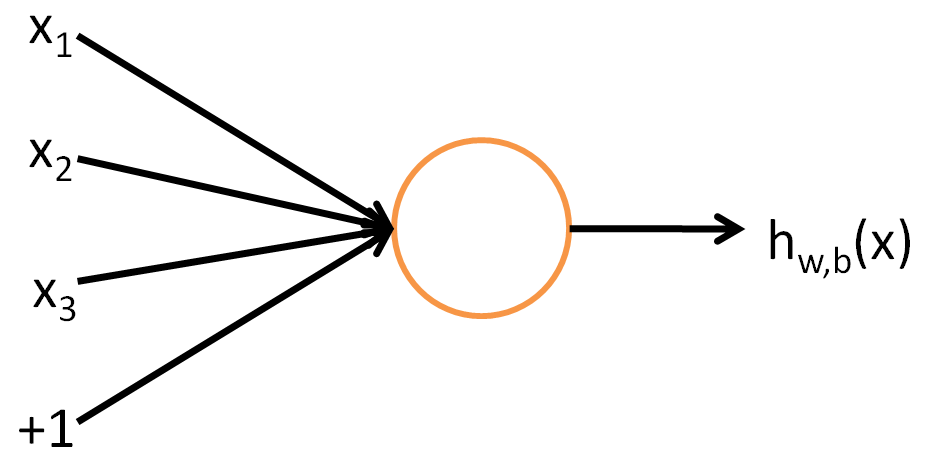
单个神经元的值实际上是前一层输入的加权线性组合

$$a_j = \sum_{i = 1}^D \omega_{ji}^{(l)}x_i +\omega_{j0}^{(l)}$$

为了使得神经网络有非线性的表达能力，需要对$a_j$进行非线性激活（线性函数级联依旧是线性函数，而线性函数不是完备基）得到神经元的输出

$$z_j = h(a_j)$$

多层神经网络就是单个神经元级联和并联的组合，隐藏神经元的值是前一层所有神经元输出的加权组合再进行非线性激活

$$a_k = \sum_{j = 1}^M \omega_{kj}^{(l+1)}z_j +\omega_{k0}^{(l+1)}，z_k = h(a_k)$$

对于输出神经元，若是回归问题，输出就是隐层的加权组合$y_k = a_k$，若是二分类问题，输出应该压缩在(0,1)，即$y_k = \sigma(a_k)$，对于多分类问题，输出可以采用softmax激活，即$y_k = softmax(a_k) $。

神经网络 vs. 感知机

感知机模型是将输入或者输入的特征进行加权组合再与分类面比较，大于0为1，小于0为-1，表达式为：

$$y_k = sign(\mathbf{w}\phi(\mathbf{x}))$$

可以抽象为如下图所示的，以符号函数为激活函数的单个神经元。

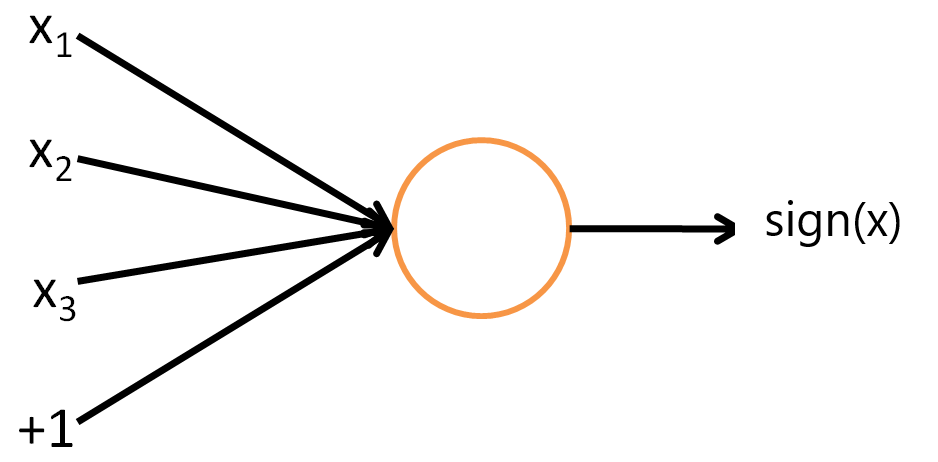
神经网络 vs. 逻辑回归

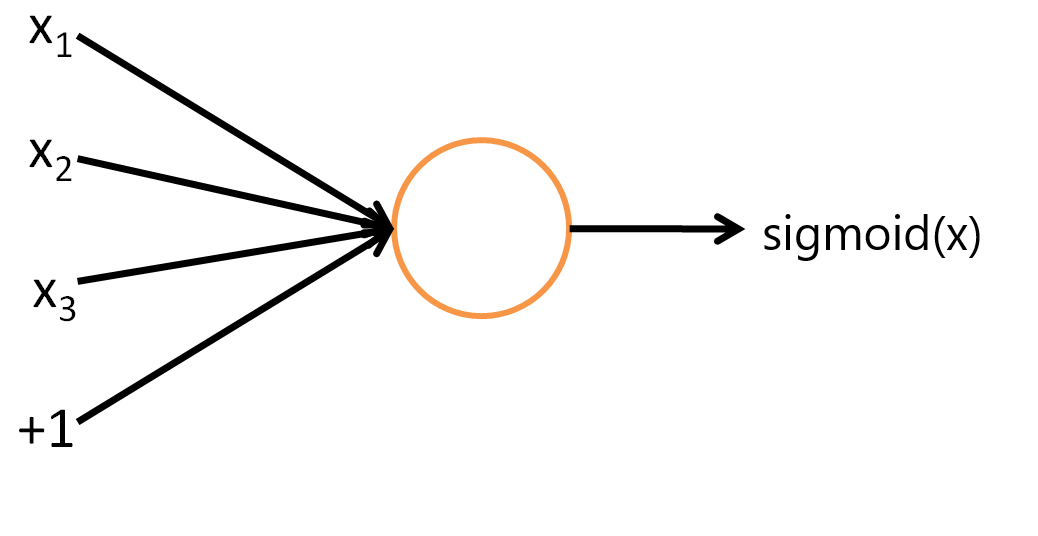
逻辑回归是将输入或者输入的特征进行加权组合，然后通过sigmoid函数转化到(0,1)

$$p(C_k|\phi) = \sigma(\mathbf{w}\phi(\mathbf{x}))$$

可以抽象为以sigmoid函数为激活函数的神经元。

神经网络实现XOR

前面的讨论中我们提到过，逻辑回归和感知机等模型都不能解决XOR问题（即(0,0)(1,1)一类，(0,1)(1,0)一类），而一个三层的神经网络，通过不同基函数（AND, ~AND, OR）的组合就可以解决XOR问题。一个简单的结果方案如下图所示：

$x_1$	$x_2$	$a_1$	$a_2$	$b$
0	0	0	1	1
0	1	0	0	0
1	0	0	0	0
1	1	1	0	1

误差的反向传播

前面我们已经讨论过了，神经网络实际上与前面的学习方法没有本质上的区别，都是对于方程的拟合，那么传统的根据训练数据调整方程表达式的序列学习方法(sequential learning)，也就是我们最常使用的(随机)梯度下降法（SGD）在神经网络的训练中同样适用。梯度下降法的表达式为

$$\mathbf{w}^{\tau+1} = \mathbf{w}^{\tau} - \eta \nabla E_n(\mathbf{w}^\tau)$$

假设采用最小均方误差来度量损失，对于一个确定模式的训练数据$x_n$

$$E_n = \frac{1}{2}\sum_k (y_{nk}-t_{nk})^2$$

多层神经网络与前面训练过程不同的地方就是隐藏层的权重与输出并没有显性的函数关系，因此输出关于隐藏层权重的微分难以表达。误差的反向传播算法实际上就是通过链式将每一层的Error转化为相同的形式，将关于权重的微分进行递归地求解。

误差传播的链式法则

一个多层神经网络后三层误差传播的示意图如下：

对于假设某个神经元输出的误差为$E_n$，对与该神经元直接相连的权重$\omega_{ji}$求偏导得

$$\frac{\partial E_n}{\partial w_{ji} } = \frac{\partial E_n}{\partial a_{j} } \frac{\partial a_j}{\partial w_{ji} }$$

记$\delta_j \equiv \frac{\partial E_n}{\partial a_{j} }$，根据前一小节的表达式$\frac{\partial a_j}{\partial w_{ji} } = z_i$

因此，上式可以写为

$$\frac{\partial E_n}{\partial w_{ji}} = \delta_j z_i$$

对于输出神经元

$$\delta_k = \frac{\partial E_n}{\partial y_{k} } = y_k - t_k$$

对于隐藏层神经元，对误差求偏导可以得到

$$\delta_j \equiv \frac{\partial E_n}{\partial a_{j}} = \sum_k \frac{\partial E_n}{\partial a_{k}} \frac{\partial a_k}{\partial a_{j}}$$

其中 $\frac{\partial E_n}{\partial a_{k} } = \delta_k$，再根据$a_k = \sum_j \omega_{kj} h(a_j) $，可以得到

$$\delta_j = h'(a_j)\sum_k \omega_{kj}\delta_k$$

根据上面的表达式，每一个神经元的误差$\delta_j$可以利用上一层神经元的误差递推地求出，进而更新权重得

$$w_{ji}^{\tau+1} = w_{ji}^{\tau} - \eta \delta_j^{\tau} z_i^{\tau}$$

神经网络的正则化方法

神经网络的表达能力很强带来的负面效果就是容易过拟合，一个隐藏层神经元的网络就可以表达非常复杂的函数形式。

这一部分将介绍几种典型的神经网络正则化方法和它们的理论依据。

高斯先验的相容性

对于一个训练好的最优的神经网络，如果将输出样本都进行如下的线性变换

$$x_i \rightarrow \tilde{x_i} = ax_i + b$$

那么我们只需要将第一层的权重和偏差进行如下的相反的线性变换，整个网络的输出将会和原网络相同。

$$\omega_{ji} \rightarrow \tilde{\omega_{ji} } = \frac{1}{a}\omega_{ji}$$ $$\omega_{j0} \rightarrow \tilde{\omega_{j0} } = \omega_{j0} - \frac{b}{a}\sum_i\omega_{ji}$$

同理，如果将输出标签进行线性变换

$$y_k \rightarrow \tilde{y_k} = cy_k + d$$

对最后一层网络进行如下变换，输出依旧与网络相同

$$\omega_{kj} \rightarrow \tilde{\omega_{kj}} = c\omega_{ji}$$ $$\omega_{k0} \rightarrow \tilde{\omega_{k0}} = c\omega_{k0} + d$$

传统统计机器学习中的正则化方法是简单地再误差函数加入权重的二范数作为正则化项

$$\tilde{E}(\mathbf{w}) = E(\mathbf{w}) + \frac{\lambda}{2}\mathbf{w}^\mathrm{T}\mathbf{w}$$

二范数的正则化从贝叶斯理论出发，实际上就是对权重给出了一个正态先验，通过后验概率表示误差函数。所谓高斯先验的相容性指的是，当所有权重的先验相同的时候，学习得到的权重也趋向于比较接近的值（同一个高斯分布内），从集合上表示就是权重的值趋向于选择在正则化项约束的超球面的表面，如下图所示。

而当对输入和输出做前面所讲的线性变换以后，由于对所有参数被统一高斯先验的约束，趋向于选择相思的值，最中的训练结果将无法得到前面所说的只改变一层网络的最优解。解决这个问题比较简单也比较常用的方法是对每一层给出不同的先验

$$p(\mathbf{w}) \propto \mathrm{exp}\left( -\frac{1}{2}\sum_k \alpha_k\|\mathbf{w}\|_k^2 \right)$$

当改变输出或者输入的时候我们只需要改变相应层的约束$\alpha_k$，前面的那种方式得到的可行解就能够被纳入解空间，这种方法在现在的深度学习框架中也比较常用（每一层设置不同的weight_decay）。

早停止

早停止这种方式比较直接，在训练数据中分出一部分作为验证集(validation)。训练过程中训练集的loss会不断下降，但是过拟合以后验证集的loss会开始上升。我们可以选择在验证集取得最小值的时候停止训练过程。

不变性

不变性指的是让网络对轻微变化数据有一定的容忍能力，这样当数据发生某些可以容忍变化的时候网络也能正确区分。比如在手写字的识别中，写在不同位置的6或者旋转了一定角度的6都应该被识别成6。这方面主要有四种手段。

切线传播

切线传播的本质就是在在正则化项中加入惩罚项，惩罚当输入数据发生特定变换的时候（比如，平移或旋转）网络输出发生的改变。假设这种变换由参数$\xi$控制，对于不同的输入，变换可以用函数$\mathrm{s} (\mathrm{x}_n, \xi)$表示。

向量发生微小的变化的变化量在数学上就可以用函数在某一点的切线斜率（导数）来描述。

记变换对$\xi$的导数在$\xi = 0$处为

$$\tau_n = \left. \frac{\partial s(x_n,\xi)}{\partial \xi}\right|_{\xi=0}$$

第$k$个输出对$\xi$的偏导为

$$\left.\frac{\partial y_k}{\partial \xi}\right|_{\xi=0} = \left.\sum_{i=1}^D \frac{\partial y_k}{\partial x_i}\frac{\partial x_i}{\partial \xi}\right|_{\xi=0} = \sum_{i=0}^D J_{ki}\tau_i$$

我们希望

$$\left.\frac{\partial y_k}{\partial \xi}\right|_{\xi=0}\rightarrow 0$$

将偏导的平方作为损失函数的正则化项，即

$$\Omega = \frac{1}{2}\sum_n\sum_k \left( \left.\frac{\partial y_{nk}}{\partial \xi}\right|_{\xi=0} \right)^2 = \frac{1}{2}\sum_n\sum_k \left( \sum_{i=0}^D J_{ki}\tau_i \right)^2$$

得到新的损失函数为

$$\tilde{E} = E + \lambda\Omega$$

变换输入样本扩展数据集（Data Augmentation)

这种方法是我们在实际操作中最常用的方法，采用神经网络需要大量充分的训练数据本质上也是模拟数据发生变换的过程。这种方法在实际操作上比较直接，在这里我们希望讨论的是它与切线传播的关系。

假设变化后的数据输入网络产生的误差函数为

$$\tilde{E} = \frac{1}{2}\iiint \{ y(s(x,\xi)) - t \}^2p(t|x)p(x)p(\xi)\mathrm{d}x\mathrm{d}t\mathrm{d}\xi$$

对变换函数$(y(s(x,\xi))-t)^2$在$\xi=0$进行二阶泰勒展开得（这里为了推导方便支队单变量的x进行展开的示例，当x为向量时，将函数按照矩阵函数表达即可）

$$\begin{split} \tilde{E} &= \frac{1}{2}\iint \{ y(x) - t \}^2p(t|x)p(x)\mathrm{d}x\mathrm{d}t\\ &+ \mathbb{E}[\xi]\iint \{ y(x) - t \}\tau \nabla y(x) p(t|x)p(x)\mathrm{d}x\mathrm{d}t\\ &+ \mathbb{E}[\xi^2]\iint \left[\{ y(x) - t \} \frac{1}{2} \left\{ \tau' \nabla y(x) +\tau \nabla \nabla y(x)\tau \right\}\right.\\ &+ \left. \left(\tau\nabla y(x)\right)^2 \right] p(t|x)p(x)\mathrm{d}x\mathrm{d}t + O(\xi^3) \end{split}$$

由于变换是在一个微小的范围内，且向不同方向变换数量应该接近（比如旋转顺时针逆时针都应该存在），可以认为 $\mathbb{E}[\xi] = 0 $，记$\mathbb{E}[\xi^2] = \lambda $，误差函数可以表达为标准形式

$$\tilde{E} = E + \lambda\Omega$$

其中，

$$\Omega = \int \left[\{ y(x) - \mathbb{E}[t|x] \} \frac{1}{2} \left\{ \tau' \nabla y(x) +\tau \nabla \nabla y(x)\tau \right\} + \left(\tau\nabla y(x)\right)^2 \right] p(x)\mathrm{d}x$$

根据泰勒展开的表达式 $\Omega = O(\xi^2) $，因此同第一章回归问题的求解类似，可以得到最小化$y(x)$的解为

$$y(x) = \mathbb{E}[t|x] + O(\xi^2)$$

因此，$\Omega$的第一项为0，正则化项可以化简为

$$\Omega = \frac{1}{2}\int \left(\tau\nabla y(x)\right)^2 p(x) \mathrm{d}x$$

与前面讲的切线传播正则化项的表达式对比可以发现形式完全相同！我认为这是一个非常有价值的结论，很多情况下我么的训练数据都是不足的，如果我们能写出变换的表达式，那么就不需要那么多训练数据就可以达到相同的效果。

数据预处理

数据预处理在前面的传统方法中就已经非常常用了，如果我们可以从训练数据中提取具有不变性的统一的特征，那么根据这些不变特征学习得到的表达式显然是具有不变性的。

卷积神经网络（CNN）

实现不变性的另外一种方式是将不变性加入网络结构的设计当中，具有代表性的方法就是CNN。

CNN的基本结构是由卷积层、下采样的组合以及全连接组成。所谓卷积过程，有信号处理基础的同学应该都能发信啊，实际上做的并不是“卷积”，而是“相关”或者说是滤波，通过一个滑动滤波器在输入层找到与滤波器结构最相似的结构作为特征。

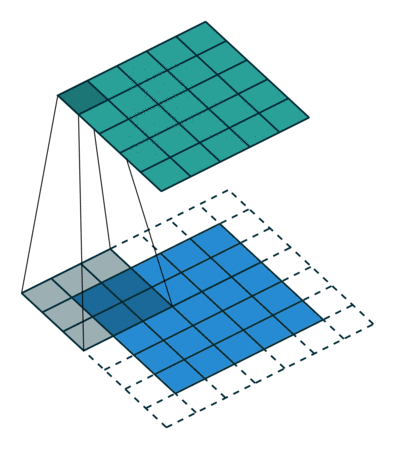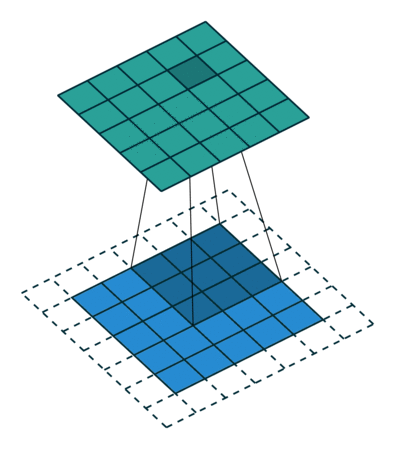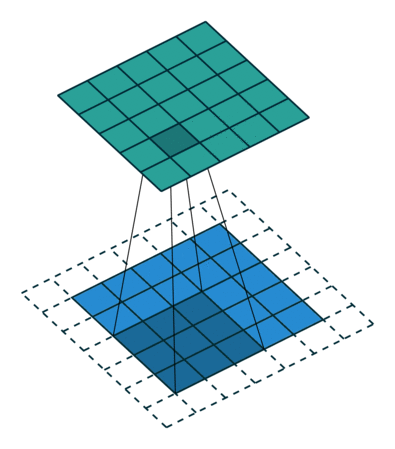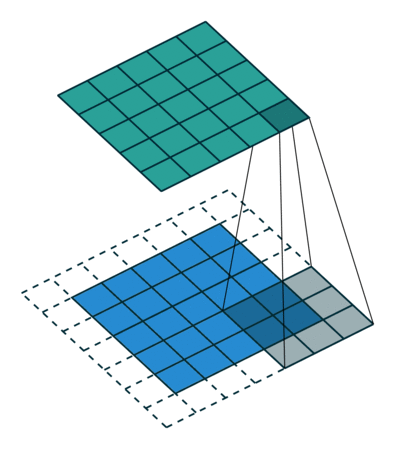
比如将下图所示的结构作为卷积核在小老鼠这副图片上进行滑动卷积

当卷积核滑动到上图所示位置时，输出单元的值6600。

当卷积核滑动到老鼠头的位置是，输出单元的值为0。这个过程说明了卷积的效果实际上就是在输入空间中寻早与卷积核相同的结构，这也引出了局部感受野的概念。

所谓局部感受野就是我们无法直接看到一副图像的全貌，但是我们可以看到很多个细节。我们认为一副图片是一张脸不需要这张脸长的一样，只需要这副图片上有眼有鼻子有嘴就可以了。

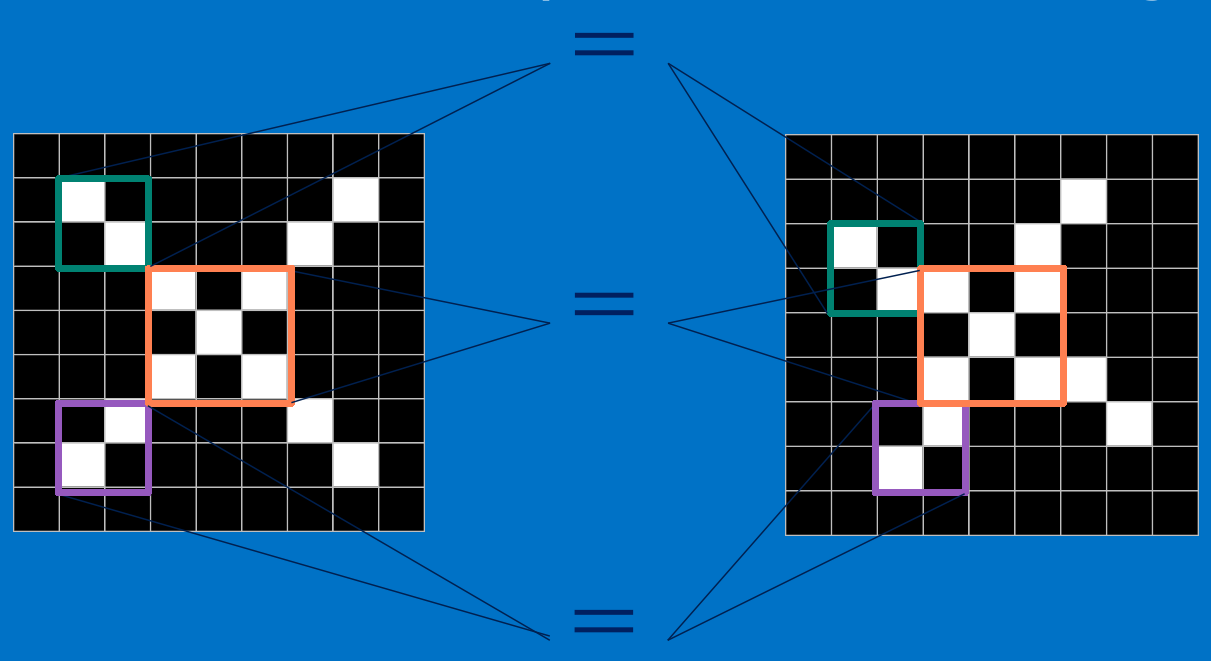
比如说上图的两个x，形状完全不同，但是我们如何能判断出右图的也是一个x呢？如果将右图的x分块我们就可以发现左右两个x的基本结构都是完全相同的。我们如果能判断这些基本结构是否存在，它们的相对位置是否相同就可以判断出这是一个x。

滑动卷积的另一个效果就是实现了权值共享，通过一个卷积核作为权重在整个图上滑动，一方面实现了不变特征的提取，另一方面也减小了参数的数量。

卷积层之后通常连接下采样层，下采样层的作用是用均值或者最大值代表一个区域内特征检测的结果，进一步提升对于局部特征变换的容忍程度，通过网络结构实现不变性。

由于CNN网络结构所带来的不变性本身就可以在一定程度上客服过拟合，因此CNN可以做的很深进一步提升表达能力。深度CNN可以通过多个卷积层的级联提取到不同尺度，不同抽象程度的特征。

软权值共享

卷积神经网络实现了权值共享，让某一层的所有神经元的权重都一致，都是该层卷积核的值，从而减小了参数的数量，同时实现了网络的不变性。但是这种方式只适用于特征只是是局部相关的先验的条件下。1992年Hinton提出了软权值共享这个概念，将对于权重完全相等的强约束转化为在每一组权重服从相同的正态分布，每一组权重趋向于取到相似的值。

假设权重可以独立的分成多个组，每个组的分布都可以用混合高斯模型来描述。即

$$p(\mathrm{w}) = \prod_i p(w_i)$$

其中，

$$p(\omega_i) = \sum_{j=1}^M \pi_j \mathcal{N}(\omega_i|\mu_j, \sigma_j^2)$$

将这个混合先验作为误差函数的正则化项

$$\Omega(w) = -\sum_i \ln \left( \sum_{j=1}^M \pi_j \mathcal{N}(\omega_i|\mu_j, \sigma_j^2) \right)$$

将比例系数$\pi_k$看作隐含变量的先验$p(z_k=1) = \pi_k$，优化过程可以通过EM算法实现。

记

$$\gamma_j(w) \equiv p(z_j=1|w_j) = \frac{\pi_j \mathcal{N}(w|\mu_j, \sigma_j^2) } {\sum_k \pi_k \mathcal{N}(w|\mu_k, \sigma_k^2) }$$

正则项对权重的微分为

$$\begin{split} \frac{\partial \Omega }{\partial w_i } &= \frac{1}{\sum_k \pi_k \mathcal{N}(w|\mu_k, \sigma_k^2)} \sum_j \pi_j \mathcal{N}(w|\mu_j, \sigma_j^2)\frac{\omega_i-\mu_j }{\sigma_j^2}\\ &= \sum_j \gamma_j(w_i)\frac{w_i-\mu_j}{\sigma_j^2} \end{split}$$

这说明权重趋向于第$j$组高斯分布的均值，这也是我们希望的，每一组内的权重趋向于相似的值。

正则项对于高斯分布均值的微分为：

$$\frac{\partial \Omega }{\partial \mu_j } = \sum_i \gamma_j(\omega_i)\frac{\mu_j-w_i}{\sigma_j^2}$$

这个结果的直觉上的解释就是高斯分布的均值趋向于组内权重的加权平均，权重正比于给定权值的第$j$组高斯分分布的后验概率。

相似的，正则化项关于标准差的微分为

$$\frac{\partial \Omega }{\partial \sigma_j } = \sum_i \gamma_j(\omega_i)\left(\frac{1}{\sigma_j }-\frac{(w_i-\mu_j)^2}{\sigma_j^3}\right)$$

它将$\sigma_j$拉向权重在对应中心$\mu_j$附近偏差的平方的加权平均，权重也是第$j$个高斯分量产生的权值参数的后验概率。

以上为第五章讨论班内容整理，希望对大家有所帮助。