作者：韩歆哲

什么是前馈神经网络

对于模式识别主要有两类问题

• 分类: 找到一个分类方程；
• 回归：找到一个回归方程。
  他们的本质都是学习得到一个能够解决问题的方程表达式。

  神经网络的基本结构与传统统计机器学习方法的关系

  前面讨论过的传统统计学习方法，包括LR，感知机等模型，本质上是将变量本身，或者通过变量组合得到的特征（基函数）进行线性组合得到线性或者非线性的分类界面：

$$y(\mathrm{x}, \mathrm{w}) = f\left( \sum_{j=1}^M \omega_j\phi_j( \mathrm{x} ) \right)$$

作者：郁博文

引论

线性分类器不同类别的样本间的决策界是超平面。

$$g({\bf x})={\bf w^T x}+x_0=g_1({\bf x})-g_2({\bf x})\tag{1}$$ $$\begin{cases}g({\bf x})>0,&\text{${\bf x}\in w_1$ }\\g({\bf x})<0,&\text{${\bf x}\in w_2$ }\\g({\bf x})=0,&\text{随机}\end{cases}$$

方程$g({\bf x})=0$定义了一个D-1维决策面(D是$\bf x$的维数，如果$\bf x$在决策面上，那么给定任意D-1维数据，$\bf x$的剩下一维都唯一确定)，将属于类别$w_1$的样本和属于类别$w_2$的样本分割开，当$g({\bf x})$是关于${\bf w}$的线性函数时，该决策面为超平面。$\bf w$是该超平面的法向量，设$\bf x_1、\bf x_2$是超平面上的任意两点，则有$g({\bf x_1})-g({\bf x_2})=\bf w^T(x_1-x_2)=0$，所以$\bf w$和超平面上的任意向量正交，法向量指向超平面的正向，即$g({\bf x})>0$的方向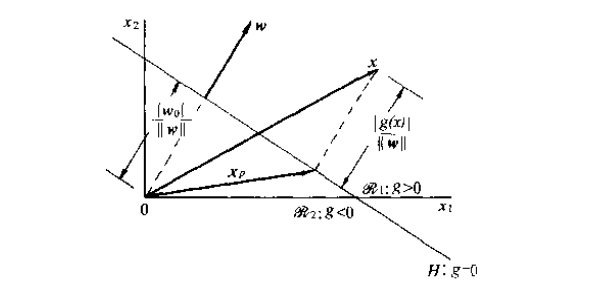

$${\bf x=x_p}+r{\bf \frac{w}{\Vert\bf w \Vert} }\tag{2}$$

$\bf x_p$是$\bf x$在超平面上的投影，r是$x$到超平面的距离，$\frac{w}{\Vert\bf w \Vert}$是单位法向量，带入式(1)可得：

$$g({\bf x})={\bf w^T x_p}+w_0+r{\bf\frac{w^Tw}{\Vert\bf w \Vert} }=r{\bf \Vert\bf w \Vert}\Rightarrow r=\frac{g({\bf x})}{\bf \Vert\bf w \Vert}$$

如果r>0，在法向量的正方向，类别1，反之类别2

作者：王愚德

频率学派

1.基础线性模型

在线性回归问题中，最简单的线性模型为：

$$y(\mathbf{x},\mathbf{w})=\mathbf{w}^\mathrm{T}\mathbf{x}=w_0+w_1x_1+\cdots+w_Dx_D$$

其中 $\mathbf{x}$为输入数据，$\mathbf{w}$为所求线性模型参数。
将上述模型进行扩展，$\mathbf{x}$可由多个$\mathbf{x}$的函数取代：

$$y(\mathbf{x},\mathbf{w}) = \mathbf{w}^\mathrm{T}\phi(\mathbf{x})= w_0+\sum_{j=1}^{M-1}w_j \phi_j(\mathbf{x})$$